浅谈ransac算法

n  RANSAC算法

RANdom SAmple Consensus（随机抽样一致）的缩写，它是根据一组包含异常数据的样本数据集，通过迭代方式估计数学模型的参数，计算出数据的数学模型参数，得到有效样本数据的算法。

对于RANSAC算法有一个基本的假设：样本中包含正确数据(inliers，符合模型的数据)和异常数据(Outliers，不符合模型的数据)，即数据集中含有噪声。这些异常数据可能是由于错误的测量、错误的假设、错误的计算等产生的。

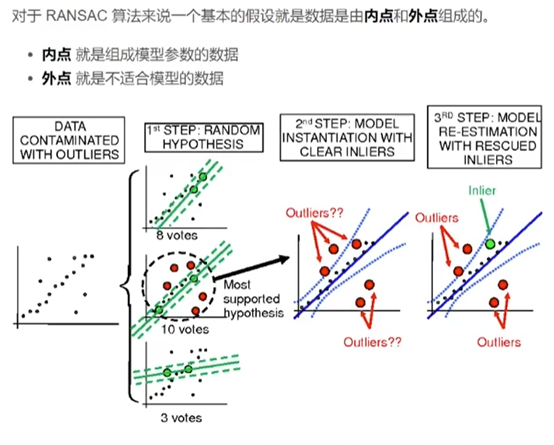
RANSAC全名为RANdom SAmple Consensus，一般译作随机抽样一致算法，是一种通用且非常成功的估计算法，它能够应付大比例野值的情况。为了可视化，我们先考虑一个简单的例子，估计一组二维点的直线拟合。具体问题可以看下图。

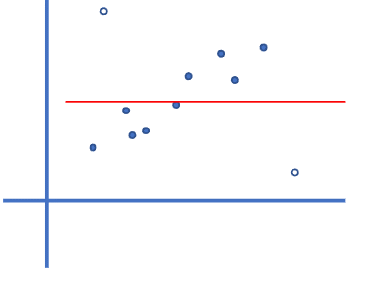
二维点直线拟合

RANSAC的目的就是排除掉那些在变换过程中出错了的那些野值点（上图中的空心点）。由于是直线拟合，故可以随机选择两个点，这两点定义一条直线，这条线的支集由在一定距离阈值内的点数来度量，随机采样重复多次，具有最 大支集的线就是鲁棒拟合，而此时在距离阈值内的点就是内点，并组成一致集。

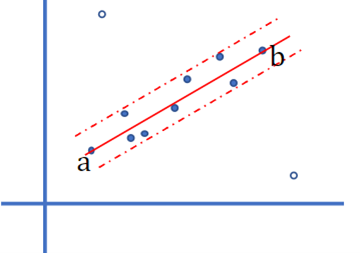
直线的鲁棒拟合

上图是一条鲁棒的拟合直线，我们选定的线的支集有9个点，它是点数最 高的直线之一，通过点数度量可以让我们排除掉直线外的野值点。更一般地说，我们希望用模型去拟合数据，随机采样出足以确定模型的最小数据集。

n  Ransac优缺点

优点：它能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。

缺点：

¡  它计算参数的迭代次数没有上限；如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。

¡  RANSAC只有一定的概率得到可信的模型，概率与迭代次数成正比。

¡  它要求设置跟问题相关的阀值。

¡  RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型，RANSAC不能找到别的模型。

¡  要求数学模型已知

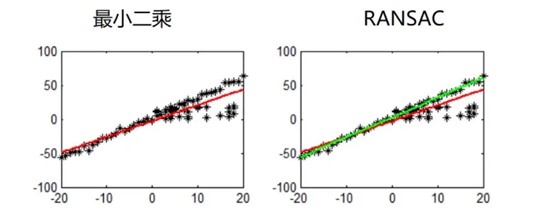
n  RANSAC和最小二乘法

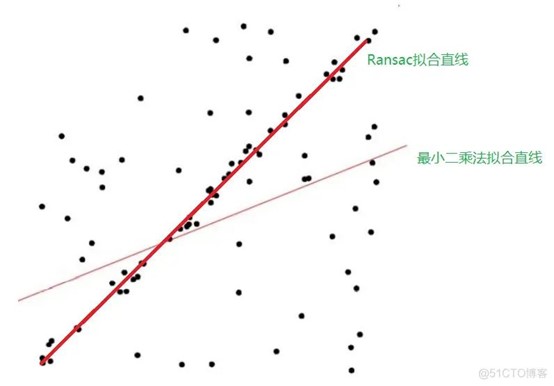
随机抽样算法（RANSAC），采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数。区别于最小二乘法，最小二乘法是考虑了所有的样本点拟合的曲线。而RANSAC是从样本点中选出几个点，拟合曲线方程，根据容忍范围来判断所“夹”住的点数，不断迭代，最终来确认目标曲线。它是根据曲线周边的样本点数，和阈值来确定的。在一定程度上，排除了最远的样本点影响。